Naive matrix multiplication Benchmark (PHP)

In my last post (PHP-SDS First thoughts) I introduced the library PHP-SDS. Today I’ll talk about some performance benchmarks that I’ve been doing in order to optimize the polyfill code.

The benchmark script has measured 8 different versions of the naive matrix multiplication algorithm:

Using array vs Using Ds\Vector.
Contiguous values vs Nested rows
I,J,K iteration order vs I,K,J iteration order.

I didn’t try to parallelize anything in any way, since PHP isn’t a well suited language to do this sort of things. I didn’t try to implement the Strassen algorithm neither, because first I want to have a solid baseline to compare (and because at some point, the Strassen algorithm should fallback to the naive algorithm).

Scripts used to benchmark and present data:

Expectations vs Reality

In the first place, I should explain what my expectations were before the experiment. I thought that the best combination would be (Ds\Vector, contiguous values, I,K,J)…

But the reality didn’t match my expectations, the best combination was (array, contiguous values, I,K,J ).

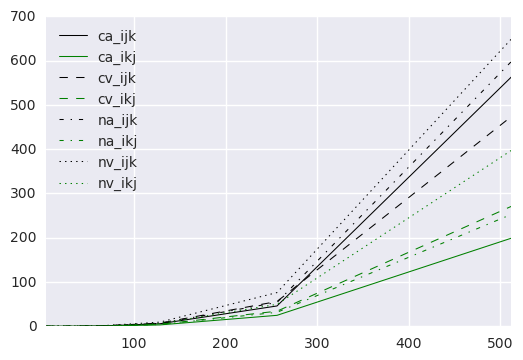
Matrix Benchmark

Why I thought that Ds\Vector would offer better performance than array for matrix multiplications? The two main reason were the smaller memory footprint, and the better performance of Ds\Vector on other operations.

I imagined that less memory usage would lead to less cache misses, but probably I missinterpreted WHY Ds\Vector uses less memory than array. The reason was not that Ds\Vector uses less bytes per item, but that Ds\Vector uses a “smarter”¹ algorithm to allocate memory regions in order to grow o shrink itself.

Why I,K,J runs faster than I,J,K?

Why my other two guesses were right? Well, it’s because the CPU cache.

Using a single data structure we avoid one indirection per read, and we can take more advandatge of data locality.
Traversing the matrix instances with the I,K,J order we ensure a row-by-row order (and even better, we can avoid some redundant read operations). This way we have a cache-oblivious algorithm.

Final thoughts

There are some benchmarks that I’d like to do in order to have a more precise image of what’s happening with Ds\Vector. I’ll measure isolated offsetGet and offsetSet operations, and a combination of both (using += for example).

Returning to my beloved matrix… In a fantastic @nikic’s post (PHP’s new hastable implementation), we can see that packed PHP arrays consume ~32 bytes per item. The Matrix use-case is “good” enough¹ to allow us storing raw values without using wrappers.

Typically, long & double values take 8 bytes in 64 bit systems, so using a compiled extension we should be able to divide the memory footprint by 4 (and store 4 times more items per cache line). If we allow less precision (using 32 bits instead of 64), then we can use less CPU time and memory.

See you soon!

Notes

Because it can rely on some assumptions that aren’t true for array.